Question

Use any of the methods to determine whether the series converges or diverges. Give reasons for your answer.

∑[infinity]n=17n2−4n+3
12+2n6

Answer 1

It means
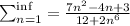`\sum_(n=1)^\inf} = (7n^2-4n+3)/(12+2n^6)` also converges.

Explanation:

The actual Series is::

`\sum_(n=1)^\inf} = (7n^2-4n+3)/(12+2n^6)`

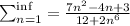
The method we are going to use is comparison method:

According to comparison method, we have:

`\sum_(n=1)^(inf)a_n\ \ \ \ \ \ \ \ \sum_(n=1)^(inf)b_n`

If series one converges, the second converges and if second diverges series, one diverges

Now Simplify the given series:

Taking"n^2"common from numerator and "n^6"from denominator.

`=(n^2[7-(4)/(n)+(3)/(n^2)])/(n^6[(12)/(n^6)+2]) \\\\=([7-(4)/(n)+(3)/(n^2)])/(n^4[(12)/(n^6)+2])`

`\sum_(n=1)^(inf)a_n=\sum_(n=1)^(inf)([7-(4)/(n)+(3)/(n^2)])/([(12)/(n^6)+2])\ \ \ \ \ \ \ \ \sum_(n=1)^(inf)b_n=\sum_(n=1)^(inf) (1)/(n^4)`

Now:

`\sum_(n=1)^(inf)a_n=\sum_(n=1)^(inf)([7-(4)/(n)+(3)/(n^2)])/([(12)/(n^6)+2])\\ \\\lim_(n \to \infty) a_n = \lim_(n \to \infty) ([7-(4)/(n)+(3)/(n^2)])/([(12)/(n^6)+2])\\=(7-(4)/(inf)+(3)/(inf))/((12)/(inf)+2)\\\\=(7)/(2)`

So a_n is finite, so it converges.

Similarly b_n converges according to p-test.

P-test:

General form:

`\sum_(n=1)^(inf)(1)/(n^p)`

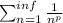
if p>1 then series converges. In oue case we have:

`\sum_(n=1)^(inf)b_n=(1)/(n^4)`

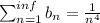
p=4 >1, so b_n also converges.

According to comparison test if both series converges, the final series also converges.

It means
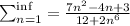`\sum_(n=1)^\inf} = (7n^2-4n+3)/(12+2n^6)` also converges.