Answer:
The result of recursive multiplication algorithm is 5332114 . Here karatsuba algorithm with recursive approach is used to compute XY where X = 1234 and Y = 4321.
Step-by-step explanation:
The steps for karatsuba algorithm with recursive approach:
base case:
if(X<10) or (Y<10) then multiply X with Y
For example if X is 1 and Y is 2. Then XY = 1*2 = 2
Recursive case:
Now when the above if condition is not true then follow these steps to compute XY
Compute the size of numbers.
Notice that there are 4 digits in X i.e. 1 2 3 4 and a 4 digits in Y i.e. 4 3 2 1
So n = 4
Now divide the numbers in 2 parts as:
n/2 = 4/2 = 2
Since these are decimal numbers so we can write it as:
10^n/2
Now split the digits
X = 1234 is divided into 2 parts as:
12 and 34
Let a represent the first part and b represent the second part of X. So,
a = 12
b = 34
Y = 4321 is divided into 2 parts as:
43 and 21
Let c represent the first part and d represent the second part of Y. So,
c = 43
d = 21
Let multiplication reprsents the karatsuba recursive multiplication algorithm
Now recursively compute products of inputs of size n/2
multiplication (a, c)
multiplication (b, d)
multiplication (add(a, b), add(c, d))
Combine the above 3 products to compute XY
As we know these decimal numbers have base 10 and X and Y are divided into two parts So X can be written as:
X =
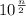 a+b
a+b
Y can be written as:
Y =
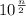 c+d
c+d
Now compute XY as:
XY = (
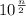 a+b) (
a+b) (
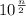 c+d)
c+d)
XY =
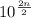 ac +
ac +
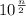 ad +
ad +
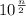 bc + bd
bc + bd
=
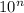 ac +
ac +
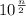 (ad + bc) + bd
(ad + bc) + bd
Now put the values of n = 4, a = 12, b = 34 , c = 43 and d = 21
= 10⁴ (12*43) + 10² (12*21 + 34*43) + (34*21)
= 10⁴ (516) + 10² (252 + 1462) + 714
= 10000*516 + 100*1714 + 714
= 5160000 + 171400 + 714
XY = 5332114
Hence the karatsuba multiplication algorithm with recursive appraoch computes XY = 5332114