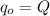Question

A hollow conductor carries a net charge of ++3QQ. A small charge of −−2QQ is placed inside the cavity in such a way that it is isolated from the conductor. How much charge is on the outer surface of the conductor?

Answer 1

The value is
`q_o = Q`

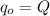
Step-by-step explanation:

From the question we are told that

The net charge is
`Q = + 3Q`

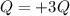
The charge place on the inside of the cavity is
`q = -2Q`

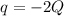
Since we are told from the question that small charge placed inside the cavity is isolated from the conductor

Then it implies that the electric flux is Zero

Which mean that the charge place within the conductor + the charge on the inner region of the conductor = 0

i.e

`q + q_i = 0`

=>
`-2Q + q_i = 0`

=>
`q_i = 2Q`

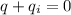
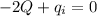
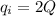
Now the net charge on the conductor is mathematically represented as

`Q = q_o + q_i`

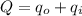
Here
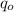`q_o` is the charge on the outer surface

So

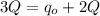
`3Q = q_o + 2Q`

=>
`q_o = Q`