Question

asked Mar 9, 2021 206k views

1 Answer

Krishan · Answer 1 · 2021-03-14T16:39:01+0000

Answer:

Explanation:

From the given information:

The present value of the house = 128000

interest rate compounded monthly r = 7.8% = 0.078

number of months in a year n= 12

duration of time t = 30 years

To find their regular monthly payment, we have:

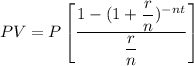
$PV = P \begin {bmatrix} (1 - (1 + (r)/(n))^(-nt))/((r)/(n)) \end {bmatrix}$

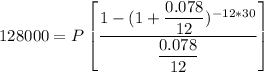
$128000 = P \begin {bmatrix} (1 - (1 + (0.078)/(12))^(- 12*30))/((0.078)/(12)) \end {bmatrix}$

128000 = 138.914 P

P = 128000/138.914

P = $921.433

∴ Their regular monthly payment P = $921.433

To find the unpaid balance when they begin paying the $1400.

when they begin the payment ,

t = 30 year - 5years

t= 25 years

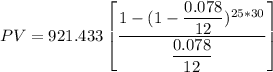
$PV= 921.433 \begin {bmatrix} (1 - (1 - (0.078)/(12))^(25*30))/((0.078)/(12)) \end {bmatrix}$

PV = $121718.2714

C) In order to estimate how many payments of $1400 it will take to pay off the loan, we have:

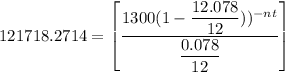
$121718.2714 = \begin {bmatrix} (1300 (1 - (12.078)/(12)))^(-nt))/((0.078)/(12)) \end {bmatrix}$

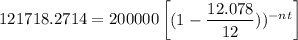
$121718.2714 = 200000 \begin {bmatrix} (1 - (12.078)/(12)))^(-nt) \end {bmatrix}$

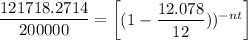
$(121718.2714)/(200000 ) = \begin {bmatrix} (1 - (12.078)/(12)))^(-nt) \end {bmatrix}$

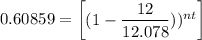
$0.60859 = \begin {bmatrix} (1 - (12)/(12.078)))^(nt) \end {bmatrix}$

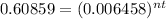
0.60859 = (0.006458)^(nt)

nt = (0.60859)/(0.006458)

nt = 94.238 payments is required to pay off the loan.

How much interest will they save by paying the loan using the number of payments from part (c)?

The total amount of interest payed on $921.433 = 921.433 × 30(12) years

= 331715.88

The total amount paid using 921.433 and 1300 = (921.433 × 60 )+( 1300 + 94.238)

= 177795.38

The amount of interest saved = 331715.88 - 177795.38

The amount of interest saved = $153920.5

Please log in or register to add a comment.