Question

Perform long division on the​ integrand, write the proper fraction as a sum of partial​ fractions, and then evaluate the integral.

2x3 - 2x + 1/x2 - 2x dx

Answer 1

`x^2+4x -(1)/(2) lnx + (2)/(13) ln(x-2) + C`

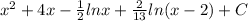
Explanation:

Given the integrand
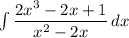`\int\limits{(2x^3 - 2x + 1)/(x^2-2x) } \, dx`, before evaluating the integral function, we will need to simplify the function first by applying long division as shown in the attachment.

Hence the partial form of the function
`(2x^3 - 2x + 1)/(x^2-2x) } = 2x+4 + (6x+1)/(x^2-2x)`

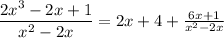
Integrating its partial sum

`\int\limits (2x^3 - 2x + 1)/(x^2-2x) }dx = \int\limits (2x+4 + (6x+1)/(x^2-2x))\ dx\\\\= \int\limits {2x} \, dx + \int\limits {4} \, dx + \int\limits {(6x+1)/(x^2-2x) \, dx\\ = (2x^2)/(2)+4x -(1)/(2) \int\limits{(1)/(x) } \, dx + (2)/(13) \int\limits{(1)/(x-2) } \, dx`

`= (2x^2)/(2)+4x -(1)/(2) lnx + (2)/(13) ln(x-2) + C`

`= x^2+4x -(1)/(2) lnx + (2)/(13) ln(x-2) + C`

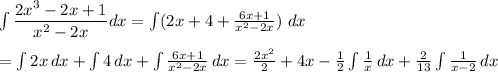
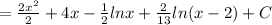
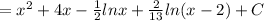
NB: Find the partial sum calculation also in the attachment.