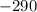Answer:
Option D,
Explanation:
Step 1: Determine the equation
We know that the initial value is 7 so that will be our starting point in the equation. We can also see that every time we go to the next number, our number has 3 subtracted from it. Therefore, we can use n-1 which will help us determine how much we need to subtract from the initial number. Here is the recursive equation
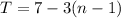
Step 2: Determine the 100th term of the sequence
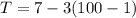
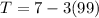
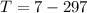

Answer: Option D,