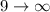Question

Consider the first order differential equation

y′ + t/t2 − 25y = et/t − 9
For each of the initial conditions below, determine the largest interval a a. y(-7) = 6.4.
b. y(-2. 5) = -0.5.
c. y(0) = 0.
d. y(4.5) = -2.1.
e. y(14)= 1.7.

Answer 1

For y(-7) =6.4

The largest interval is between

`-\infty \to -5`

For y(-2.5) = -0.5.

The largest interval is between

`-5 \to 5`

For y(0) = 0

The largest interval is between

`-5 \to 5`

For y(4.5) = -2.1.

The largest interval is between

`-5 \to 5`

For y(14)= 1.7.

The largest interval is between

`9 \to \infty`

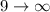
Explanation:

From m the question we are told that

The first order differential equation is
`(y' - t)/( t^2 -25) = (e^t)/(t-9)`

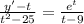
Now the first step is to obtain the domain of the differential equation

Now to do that let consider the denominators

Now generally

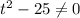`t^2 - 25 \\e 0` side calculation

=>
`t\\e \pm5`
`t^2 - 25 = 0`

`t = \pm 5`

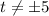
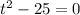
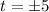
Also
`t-9\\e 0`
`t -9 = 0`

=>
`t\\e 9`
`t= 9`

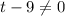
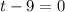
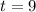
This means that this first order differential equation is discontinuous at

`t = -5 , \ \ t = 5 \ \ t = 9`

`This \ is \ illustrated \ below \ \\ ------------------\\\. \ \ \ | \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ | \ \ \ \ \ \ \ \ \ \ \ \ \ |\\. \ -5 \ \ \ \ \ \ \ \ \ \ \ \ 5 \ \ \ \ \ \ \ \ \ \ \ \ \ 9`

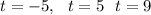
So

For y(-7) =6.4

The largest interval is between

`-\infty \to -5`

For y(-2.5) = -0.5.

The largest interval is between

`-5 \to 5`

For y(0) = 0

The largest interval is between

`-5 \to 5`

For y(4.5) = -2.1.

The largest interval is between

`-5 \to 5`

For y(14)= 1.7.

The largest interval is between

`9 \to \infty`