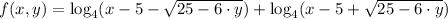Answer:
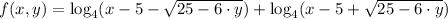
Explanation:
Let be
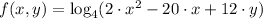 , this expression is simplified by algebraic and trascendental means. As first step, the second order polynomial is simplified. Its roots are determined by the Quadratic Formula, that is to say:
, this expression is simplified by algebraic and trascendental means. As first step, the second order polynomial is simplified. Its roots are determined by the Quadratic Formula, that is to say:
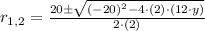
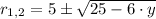
The polynomial in factorized form is:

The function can be rewritten and simplified as follows:
![f(x,y) = \log_(4) [(x-5-√(25-6\cdot y))\cdot (x-5+√(25-6\cdot y))]](https://img.qammunity.org/2021/formulas/mathematics/college/tp5rryfgow0zl6bs5cw3lyd6w2gtvulj5k.png)