Answer:
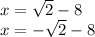
Explanation:
To complete the square, we first have to get our equation into
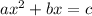 form.
form.
First we add 16x to both sides:
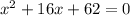
And now we subtract 62 from both sides.
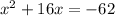
We now have to add
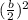 to both sides of the equation. b is 16, so this value becomes
to both sides of the equation. b is 16, so this value becomes
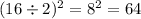 .
.
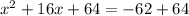
We can now write the left side of the equation as a perfect square. We know that x+8 will be the solution because
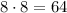 and
and
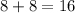 .
.

We can now take the square root of both sides.
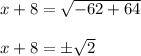
We can now isolate x on one side by subtracting 8 from both sides.
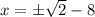
So our solutions are
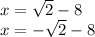
Hope this helped!