Complete Question
A NASA spacecraft measures the rate R of at which atmospheric pressure on Mars decreases with altitude. The result at a certain altitude is:
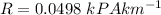 Convert R to
Convert R to
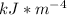
Answer:
The value is

Step-by-step explanation:
From the question we are told that
The altitude is
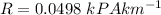
Generally
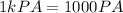
So
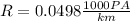
Also
1 km = 1000 m
So
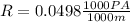
=>
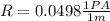
Now PA is Pascal which is mathematically represented as
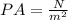
So
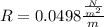
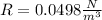
Looking the unit we are arrive at we see that it contains J which is mathematically represented as
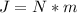
So
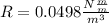
=>
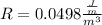
=>
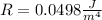
Generally
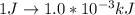

=>
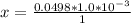
=>
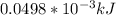
So
