Question

(a) Calculate the kinetic energy, in joules of a 1200 -kg automobile moving at 18 m/s .

(b) Convert this energy to calories.
(c) When the automobile brakes to a stop is the "lost" kinetic energy converted mostly to heat or to some form of potential energy?

Answer 1

a) The kinetic energy of the 1200-kg automobile moving at 18 meters per second is 194400 joules, b) The kinetic energy of the 1200-kg automobile moving at 18 meters per second is 46440.516 calories, c) the kinetic energy is transformed into work due to friction, which is a non-conservative force. And such work is dissipated in the form of heat.

Step-by-step explanation:

a) Let be the automobile considered as particle travelling on horizontal ground, so that motion is entirely translational and whose formula for kinetic energy, measured in joules, is:

`K = (1)/(2)\cdot m \cdot v^(2)`

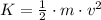
Where:

`m` - Mass, measured in kilograms.

`v` - Speed of automobile, measured in meters per second.

If
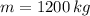`m = 1200\,kg` and
`v = 18\,(m)/(s)`, the kinetic energy of the automobile is:

`K = (1)/(2)\cdot (1200\,kg)\cdot \left(18\,(m)/(s) \right)^(2)`

`K = 194400\,J`

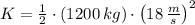
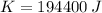
The kinetic energy of the 1200-kg automobile moving at 18 meters per second is 194400 joules.

b) A calory equals 4.186 joules. The kinetic energy in calories is:

`K = 194400\,J * \left((1)/(4.186)\,(cal)/(J) \right)`

`K = 46440.516\,cal`

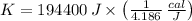
The kinetic energy of the 1200-kg automobile moving at 18 meters per second is 46440.516 calories.

c) When the automobile brakes to a stop, the kinetic energy is transformed into work due to friction, which is a non-conservative force. And such work is dissipated in the form of heat. Hence, such energy cannot be recovered. Potential energies are conservative by nature.