Answer:
A) ΔEm = 0.29, B) v₁ = 5.8 m/s, c) v₂= 4.9 m / s D) the correct answer from 4
Step-by-step explanation:
For this exercise we will use conservation of energy, taking care of how to choose our system
A) For this case we take two instants
starting point. When the ball goes out
Em₀ = U = m g y₁
Final point. When the ball reaches its maximum height
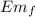 = U = m g y₂
= U = m g y₂
In this case we see that there is a loss of mechanical energy at the moment of rebound, therefore the fraction of energy lost is
ΔEm = Em_{f} / Em₀
ΔEm = mg y₂ / mg y₁
ΔEm = y₂ / y₁
ΔEm = 1.2 / 1.7
the lost part of energy
ΔEm = 1 -0.706
ΔEm = 0.29
B) the velocity just before the bounce
starting point. When the ball is released
Em₀ = U = m g y₁
final punot. Just wide of the bounce
Em_{f} = K = ½ m v₁²
As it has not yet rebounded, it has no energy loss, therefore the mechanical energy is conserved
Em₀ = Em_{f}
m g y₁ = ½ m v₁²
v₁ = √ 2 g y₁
let's calculate
v₁ =√ (2 9.8 1.7)
v₁ = 5.77 m / s
v₁ = 5.8 m/s
C) the velocity just after the bounce
starting point, after bounce
Em₀ = K = ½ m v₂²
final point. Maximum height after bounce
Em_{f} = U = m g y₂
as it already bounced, the energy is conserved in this interval
Em₀ = Em_{f}
½ m v₂² = m g y₂
v₂ = √ (2 g y₂)
v₂ = √ (2 9.8 1.2)
v₂ = 4.85 m / s
v₂= 4.9 m / s
D) during the time that the bounce lasts, there is a strong change in energy, part of it is transformed into thermal energy, due to several processes: friction, change in the potential energy of the molecules of the ball, change in the internal energy of the balls. molecules.
Therefore we cannot specify a single process, consequently the correct answer from 4