Answer:

Explanation:
So we have:
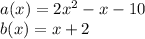
And we want to find the quotient q(x). Thus:
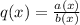
Substitute:
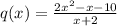
Factor the numerator:
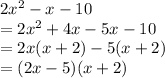
Substitute:
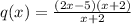
The (x+2)s cancel out. Therefore:
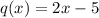
However, we must restrict x such that it cannot equal -2.
In the original equation, if it did, our answer would be undefined. Thus, our final answer is:

And we are done :)
Edit: Typo