Question

Twenty-three student compete in a math competition in which the top three studentsare recognized with trophies for first, second, and third place. How many different outcomes arethere for the top three places?

Answer 1

10626 ways

Explanation:

Given

Number of students = 23

Prizes = 3

Required

Number of different outcomes for the top 3

This question will be solved using permutation formula because it implies selection of 3 students from 23

`^nP_r = (n!)/((n-r)!)`

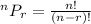
Where n = 23 and r = 3

The formula becomes

`^(23)P_3 = (23!)/((23-3)!)`

`^(23)P_3 = (23!)/((20)!)`

`^(23)P_3 = (23!)/(20!)`

`^(23)P_3 = (23 * 22 * 21 * 20!)/(20!)`

`^(23)P_3 = 23 * 22 * 21`

`^(23)P_3 = 10626`

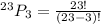
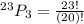
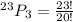
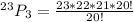
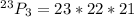
Hence, there are 10626 ways