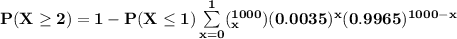Question

. Every month, there are 1000 independent TIE fighter flights, and each TIE fighter flight crashes with a probability of 0.0035. (a) What is the probability that at least 2 crashes occur in the next month

Answer 1

`\mathbf{P (X \geq 2) = 1 - P( X \leq 1) \sum \limits ^1_(x=0) ( ^(1000)_x) (0.0035)^x (0.9965)^(1000-x)}`

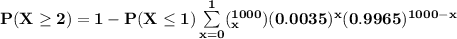
Explanation:

From the information given:

The probability that at least 2 crashes occurs in the next month can be estimated by using Poisson distribution because the sample size is large and the probability of the event p = 0.0035 is rare.

∴

Let X be the random variable that follows a Poisson distribution

The probability that at least 2 crashes occurs in the next month is:

`\mathbf{P (X \geq 2) = 1 - P( X \leq 1) \sum \limits ^1_(x=0) ( ^(1000)_x) (0.0035)^x (0.9965)^(1000-x)}`