Question

Find the equation of a sphere if one of its diameters has endpoints: (-9, -12, -6) and (11, 8, 14).

= 0

Answer 1

Hence, the equation of a sphere with one of its diameters with endpoints (-9, -12, -6) and (11, 8, 14) is
`(x-1)^(2)+(y+2)^(2)+(z-4)^(2) = 30`.

Explanation:

There are two kew parameters for a sphere: Center (
`h`,
`k`,
`s`) and Radius (
`r`). The radius is the midpoint of the line segment between endpoints. That is:

`C(x,y,z) = \left((-9+11)/(2),(-12+8)/(2),(-6+14)/(2) \right)`

`C(x,y,z) = (1,-2,4)`

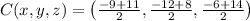
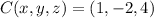
The radius can be found by halving the length of diameter, which can be determined by knowning location of endpoints and using Pythagorean Theorem:

`r = (1)/(2)\cdot \sqrt{(-9-11)^(2)+(-12-8)^(2)+(-6-14)^(2)}`

`r = 10√(3)`

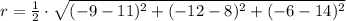
The general formula of a sphere centered at (h, k, s) and with a radius r is:

`(x-h)^(2)+(y-k)^(2)+(z-s)^(2) = r^(2)`

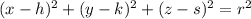
Hence, the equation of a sphere with one of its diameters with endpoints (-9, -12, -6) and (11, 8, 14) is
`(x-1)^(2)+(y+2)^(2)+(z-4)^(2) = 30`.