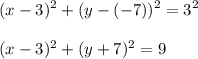Answer:
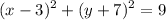
Explanation:
By looking at the graph, we can say that the circle has a center point at (3,-7). Next, find the radius which is the distance between center and an endpoint.
Distance Formula
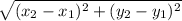
Determine:
- Center =
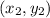 = (3,-7)
= (3,-7) - Endpoint =
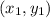 = (0,-7)
= (0,-7)
Therefore:
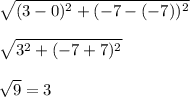
Therefore, radius = 3.
Equation of Circle
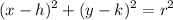
where:
- (h,k) = center = (3,-7)
- r = 3 so r² = 9
Hence: