Answer:
The linear equation relating price to demand is Q=-0.5*P + 30
Explanation:
The demand for a good is the quantity of that good that the demanders are willing to purchase at a given price.
Then, the Demand Curve relates the quantity that a consumer would be willing to buy as a function of price.
You seek to determine the linear equation that relates the price to the demand Q = m * P + b where Q is the quantity demanded at a price P, and compared with the equation of the straight line y = mx + b, m is the slope and b is the ordinate to the origin.
On a line of the form y = m * x + b, the value of m, having two points, is calculated by:
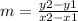
And the ordinate to the origin b is calculated, taking the value of m, replacing any of the two points (replacing any of the two because it must give the same value of b) in the expression y = m * x + b and solving its value.
In the case of Q=m*P+b, the value of m, having two points, is calculated by:
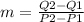
Being:
- Q1= 5
- P1= $50
- Q2= 10
- P2= $40
and replacing:

you get:
m= -0.5
So, being Q=-0.5*P+b, b is calculated by:
- Replacing the point Q1= 5 and P1= 50
5= -0.5*50 + b → 5= -25 + b → 5+25= b → b= 30
- Replacing the point Q1= 10 and P1= 40
10= -0.5*40 + b → 10= -20 + b → 10+20= b → b= 30
Then, the linear equation relating price to demand is Q=-0.5*P + 30