Question

`x - 2√(x - 3 = 0)`
what value of x satisfies the equation above?
x=​

Answer 1

No Real Solutions

Explanation:

So we have:

`x-2√(x-3)=0`

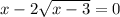
First, determine the domain restrictions. The expression under the radical cannot be less than 0. Therefore:

`x-3\geq 0\\x\geq 3`

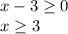
Therefore, our final answers must be greater than or equal to 3:

Now, going back to the original equation, subtract x from both sides:

`-2√(x-3)=-x`

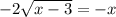
Now, square both sides:

`4(x-3)=x^2`

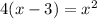
Distribute:

`4x-12=x^2`

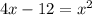
Subtract 4x and add 12 to both sides:

`0=x^2-4x+12`

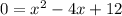
This isn't factor-able. Let's use the quadratic formula. a is 1, b is -4 and c is 12:

`x= (-b \pm √(b^2-4ac))/(2a)`

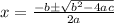
Substitute:

`x=(4\pm√((-4)^2-4(1)(12)))/(2(1))`

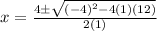
Simplify the radical:

`x=(4\pm√(-32))/(2(1))`

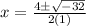
The number under the radical is negative. In other words, there are no real solutions.