Answer:
No Real Solutions
Explanation:
So we have:
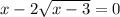
First, determine the domain restrictions. The expression under the radical cannot be less than 0. Therefore:
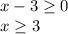
Therefore, our final answers must be greater than or equal to 3:
Now, going back to the original equation, subtract x from both sides:
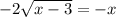
Now, square both sides:
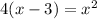
Distribute:
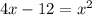
Subtract 4x and add 12 to both sides:
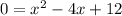
This isn't factor-able. Let's use the quadratic formula. a is 1, b is -4 and c is 12:

Substitute:
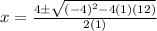
Simplify the radical:
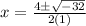
The number under the radical is negative. In other words, there are no real solutions.