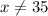Question

Jacob is a construction

worker who earns a yearly income given by the expression 2000x + 4000, where X is the number of hours
he works each week. Carlos works with Jacob and earns a yearly income given by the expression 3500x - 40000. A manager
predicts that if Carlos and jacob each work 35 hours, they will earn the same amount of money,

Answer 1

The manager's prediction is false

Explanation:

Given

Jacob: 2000x + 4000

Carlos: 3500x - 40000

Required

Determine if both expression will be the same if x = 35

To do this;

Equate both expressions and then solve for x

i.e.

`2000x + 4000 = 3500x - 40000`

Collect Like Terms

`2000x - 3500x = -4000 - 40000`

`-1500x = -44000`

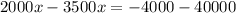
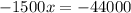
Divide both sides by -1500

`(-1500x)/(-1500) = (-44000)/(-1500)`

`x = (-44000)/(-1500)`

`x - 29.3`

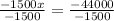
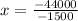
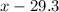
Hence, the manager's prediction is not true because
`x \\eq 35`