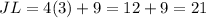Question

Point K is on line segment JL. Given KL = 2x – 2, JL = 4x + 9, and

JK = 5x + 2, determine the numerical length of JL. i

Answer 1

JL = 21

Explanation:

Given that K is on line segment JL, therefore:

KL + JK = JL (according to segment addition postulate)

KL = 2x - 2

JK = 5x + 2

JL = 4x + 9

Thus:

`(2x - 2) + (5x + 2) = (4x + 9)`

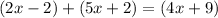
Solve for x

`2x - 2 + 5x + 2 = 4x + 9`

`2x +5x - 2 + 2 = 4x + 9`

`7x = 4x + 9`

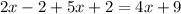
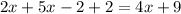
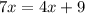
Subtract 4x from both sides

`7x - 4x = 4x + 9 - 4x`

`3x = 9`

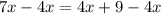
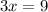
Divide both sides by 3

`(3x)/(3) = (9)/(3)`

`x = 3`

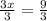
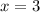
Find the numerical length of JL

`JL = 4x + 9`

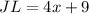
Plug in the value of x

`JL = 4(3) + 9 = 12 + 9 = 21`