Question

Let un be the nth Fibonacci number. Prove that the Euclidean algorithm takes precisely n steps to prove that gcd(un+1, un) = 1.

Answer 1

Hello, Please consider the following.

Fibonacci numbers are defined as

`u_0=1\\\\u_1=1\\\\u_(n+2)=u_(n+1)+u_(n) \ for \ n\geq 0`

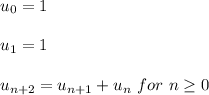
Step 1 - The proposition is true for n = 1

`GCD(u_2,u_1) ?\\`

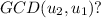
Let's apply Euclidean algorithm

`u_1=1, u_2=2\\\\u_2=2* u_1+0 = 2 * 1 +0`

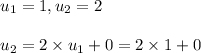
This is exactly 1 step and
`GCD(u_2,u_1) =1`

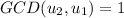
Step 2 - We assume that this is true for k, meaning that the Euclidean algorithm takes precisely k steps to prove that
`GCD(u_(k+1),u_(k))=1`

`u_(k+2)=u_(k+1)+u_k \ and \ 0 < u_k < u_(k+1)`

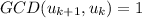
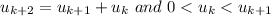
So, the first step of the algorithm is

`u_(k+2)=u_(k+1)* 1 +u_(k)`

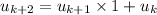
And from now, we need to find
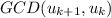`GCD(u_(k+1),u_k)` which is 1 and takes k steps, by induction Hypothesis. Therefore, it takes k + 1 steps to find
`GCD(u_(k+2),u_(k+1))=1`

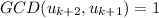
Step 3 - Conclusion

We have just proved that the Euclidean algorithm takes precisely n steps to prove that
`GCD(u_(n+1),u_(n))=1`

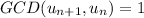
Thanks