Question

• Check your work when you're done.

Your Assignment
Michael and his sister Mel share the job of mowing the grass in their yard. Michael mows 1/3
of the yard, and Mel mows the rest. Mel can mow 3/4 of the entire yard in an hour. How long will it take Mel to finish mowing her part of the yard?

Answer 1

Approximately 53 mins

Explanation:

Yard mowed by Michael = ⅓ of the yard

Yard mowed by Mel = 1 - ⅓ =
`(1)/(1) - (1)/(3) = (3 - 1)/(3) = (2)/(3)`

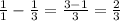
Rate at which Mel can mow a yard = ¾ of the yard in 1 hour

That is, it would take 1 hr to mow ¾ of the yard.

If ¾ yard requires 1 hr, then,

⅔ yard would require x hr

Thus:

x*¾ = 1*⅔

`(3x)/(4) = (2)/(3)`

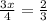
Cross multiply

`3(3x) = 4(2)`

`9x = 8`

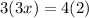
Divide both sides by 9

`x = (8)/(9)`

It would take Mel
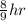`(8)/(9) hr` to finish mowing her part, which is approximately 53 mins.
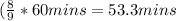`((8)/(9)*60mins = 53.3mins`.