Question

I need help finishing a question. I used the explanation function on the program, but it didn't specify what to do to get the final answer. I have attached a picture.

"Find the real solutions. Use the quadratic formula and a calculator."

At the last step, it said to use a calculator to see if the solutions satisfy the equation, but does that mean I need to plug in the whole thing for each x in the original equation? That would take a long time. I tried punching the "(1 plus or minus sqrt (1 + 160pi^2)) / 2" into my calculator, but the answers I got were wrong.​

Answer 1

I would compute sqrt(1 + 160pi^2) first to get approximately 39.75093337

Add this to 1 and we have 40.75093337

Then divide over 2pi to get a final approximate result of 6.48571248

So x = 6.48571248 is one approximate solution

In short, I computed
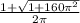`(1+√(1+160\pi^2))/(2\pi)` only focusing on the plus for now.

----------------------

If you were to compute
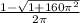`(1-√(1+160\pi^2))/(2\pi)` you should get roughly -6.167402596 as your other solution. Each solution can then be plugged into the original equation to check if you get 0 or not. You likely won't land exactly on 0 but you'll get close enough.

Answer 2

x = 6.49

Explanation:

1st is to calculate
`√(1 + 160 pi^2)` = 39.75 then add 1 = 40.75

2nd divide it by 2pi = 40.75/(2pi) = 6.49

therefore your x = 6.49

the equation would look like

1 ±
`√(1 + 160 pi^2)` 1 ± 39.75

= -------------------------- = ---------------- = 6.49

2*pi 6.28