Question

17. The owner of an organic fruit stand also sells nuts. She wants to mix cashews worth $5.50 per pound with peanuts worth

$2.30 per pound to get a 1/2 pound mixture that is worth $2.80 per pound. How much of each kind of nut should she include
in the mixed bag?
A. Cashews: 0.10 lb.; peanuts: 0.40 1b.
B. Cashews: 0.42 lb.; peanuts: 0.08 1b.
C. Cashews: 0.40 lb.; peanuts: 0.10 1b
D. Cashews: 0.27 lb.; peanuts: 0.23 1b.
E. Cashews: 0.23 lb.; peanuts: 0.27 1b.
F. Cashews: 0.08 lb.; peanuts: 0.42 1b

Answer 1

E

Explanation:

Let's let c denote the amount of cashews and let's let p denote the amount of peanuts.

So, the owner wants to mix cashews worth $5.50 per pound with peanuts worth $2.30 per pound to get a 1/2 pound mixture that is worth $2.80 per pound.

In other words, the total pounds as an equation is:

`c+p=0.5`

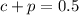
Also, the price would be:

`5.5c+2.3p=(p+c)2.8`

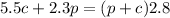
Since we mixed the peanuts and cashews, our sum would be 2.8(p+c).

And we already determined that p+c is 0.5. Thus, substitute:

`5.5c+2.3p=(0.5)(2.8)`

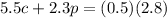
Simplify:

`5.5c+2.3p=1.4`

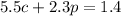
Now, we can solve the system of equations. Isolate a variable from the very first equation:

`c+p=0.5`

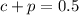
Subtract p from both sides:

`c=0.5-p`

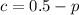
Now, substitute this into the equation earlier:

`5.5c+2.3p=1.4\\5.5(0.5-p)+2.3p=1.4`

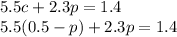
Distribute:

`2.75-5.5p+2.3p=1.4`

Combine like terms:

`2.75-3.2p=1.4`

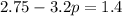
Subtract both sides by 2.75:

`-3.2p=-1.35`

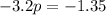
Divide everything by -3.2:

`p=0.412875`

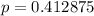
Now, find c:

`p+c=.5`

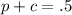
Substitute:

`c+0.421875=.5`

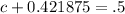
Subtract:

`c=0.078125`

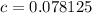
Thus, the owner would need 0.08 pounds of cashews and 0.42 pounds of peanuts.

Our answer is E.