Question

Explain please!!

12. A shipment of TV sets, some weighing 30 kg each and the other weighing 50 kg each, has a total weight of 220 kg. If there
are 20 TV sets all together, how many weigh 50 kg and how many weigh 30 kg?
A. 6 weigh 50 kg and 14 weigh 30
B. 15 weigh 50 kg and 5 weigh 30.
C. 2 weigh 50 kg and 18 weigh 30
D. 14 weigh 50 kg and 6 weigh 30
E. 4 weigh 50 kg and 16 weigh 30
F. 11 weigh 50 kg and 9 weigh 30

Answer 1

Explanation:

Total number of T..V sets we have 20

Let x be the number of T.V sets that weigh 30 kg and y be the no. of sets that weigh 50 kg

When we add all we get a total of 880

`\blue\star` 30a + 50b = 880

It is given to us that

`\blue\star`a + b = 20. eq 1

`\blue\star`a = 20-b

Put the value of a in ist equation we get,

`\blue\star`30(20-b) + 50b =880

`\blue\star`600 - 30b+50b = 880

`\blue\star`600 + 20b = 880

`\blue\star`20b = 280

`\blue\star` b = 14

so there are 14 T.V sets that weigh 50 kg

put it in eq 1 we get

`\blue\star` a + b =20

`\blue\star`a + 14 = 20

`\blue\star`a = 6

Hope it helps.

Answer 2

D

Explanation:

Let a be the number of TV sets that weight 30 kg and let b be the number of TV sets that weigh 50 kg.

So, all together, they have a total weight of 880. In other words:

`30a+50b=880`

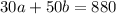
And, there are 20 TV sets all together. Thus:

`a+b=20`

This is a system of equations. Solve by substitution. Subtract b from both sides in the second equation:

`a+b=20\\a=20-b`

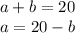
Substitute this into the first:

`30a+50b=880\\30(20-b)+50b=880`

Distribute:

`600-30b+50b=880`

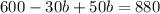
Subtract 600 from both sides:

`-30b+50b=280`

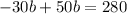
Combine like terms:

`20b=280`

Divide both sides by 20:

`b=14`

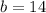
So, there are 14 TV sets that weight 50 kg.

Plug this in for the second equation to solve for a:

`a+b=20`

Plug in 14 for b:

`a+14=20`

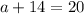
Subtract 14 from both sides:

`a=6`

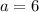
Therefore, there are 6 TV sets that weigh 30 kg and 14 TV sets that weigh 50 kg.

Our answer is D :)