Question

The limit with the steps if it exist plz

Answer 1

1/4

Explanation:

Hello, first of all we could say, let 's replace x by 1 and see if we can conclude.

numerator gives
`√(1+15)-4=√(16)-4=4-4=0`

denominator gives 1-1=0

So, this is 0/0 and this is not defined.

We need to ask a friend for help. Guillaume de l'Hôpital, French mathematician from the 1600s, has a trick to solve this kind of stuff.

In short, he says that

`\displaystyle \lim_(x\rightarrow c) \ {(f(x))/(g(x))}=\lim_(x\rightarrow c) \ {(f'(x))/(g'(x))}`

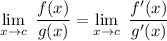
In our case here, we have c = 1

`f(x)=√(x^2+15)-4\\\\g(x)=x-1`

`f'(x)=(1)/(2)(2x)/(√(x^2+15))=(x)/(√(x^2+15))\\\\f'(1)=(1)/(4)\\\\g'(x)=1\\\\(f'(1))/(g'(1))=(1)/(4)`

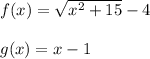
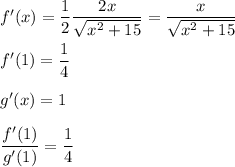
So, we can conclude

`\displaystyle \lim_(x\rightarrow1) \ {(√(x^2+15)-4)/(x-1)}=\lim_(x\rightarrow1) \ {(1)/(4)}=\boxed{(1)/(4)}`

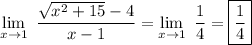
Thanks