Question

The effective spring constant describing the potential energy of the HBr molecule is 410 N/m and that for the NO molecule is 1530 N/m.A) Calculate the minimum amplitude of vibration for the NO molecule.

B) Calculate the minimum amplitude of vibration for the HCl molecule.

Answer 1

a. the minimum amplitude of vibration for the NO molecule A
`\simeq` 4.9378 pm

b. the minimum amplitude of vibration for the HCl molecule A
`\simeq` 10.9336 pm

Step-by-step explanation:

Given that:

The effective spring constant describing the potential energy of the HBr molecule is 410 N/m

The effective spring constant describing the potential energy of the NO molecule is 1530 N/m

To calculate the minimum amplitude of vibration for the NO molecule, we use the formula:

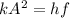
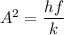
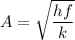
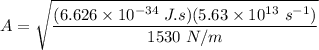
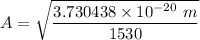
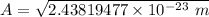
`(1)/(2)kA^2= (1)/(2)hf`

`kA^2= hf`

`A^2= (hf)/(k)`

`A = \sqrt{(hf)/(k)}`

`A = \sqrt{((6.626 * 10^(-34) \ J. s ) ( 5.63 * 10^(13) \ s^(-1)))/(1530 \ N/m)}`

`A = \sqrt{(3.730438 * 10^(-20) \ m)/(1530 )`

`A = \sqrt{2.43819477 * 10^(-23)\ m`

`A =4.93780799 * 10^(-12) \ m`

A
`\simeq` 4.9378 pm

The effective spring constant describing the potential energy of the HCl molecule is 480 N/m

To calculate the minimum amplitude using the same formula above, we have:

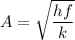
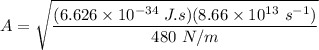
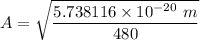
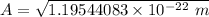
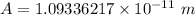
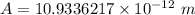
`A = \sqrt{(hf)/(k)}`

`A = \sqrt{((6.626 * 10^(-34) \ J. s ) ( 8.66 * 10^(13) \ s^(-1)))/(480 \ N/m)}`

`A = \sqrt{(5.738116* 10^(-20) \ m)/(480 )`

`A = \sqrt{1.19544083* 10^(-22)\ m`

`A = 1.09336217 * 10^(-11) \ m`

`A = 10.9336217 * 10^(-12) \ m`

A
`\simeq` 10.9336 pm