Answer:
y=3x+25
Explanation:
We are given a point and the slope, so let's use the slope-intercept equation.

where m is the slope and (x₁, y₁) is the point given. The slope is 3 and the point is (2,31). Therefore,
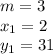
Substitute the values into the equation.
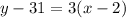
We want the equation in slope intercept form: y=mx+b. We must isolate y on the left side of the equation.
First, distribute the 3. Multiply each term inside the parentheses by 3.
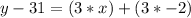
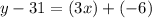
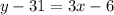
Next, add 31 to both sides of the equation.
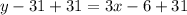
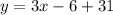
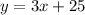
This equation is in slope intercept form, so our final answer is:
y= 3x+25 (slope⇒3 , y-intercept ⇒25)