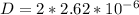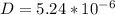Answer:
a
w = 8.46 *10^{-6} \ rad
b
D =5.24 *10^{-6}
Step-by-step explanation:
From the question we are told that
The diameter of the lens is

The focal length is
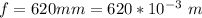
The wavelength is

Generally the angular width is mathematically represented as

Here
 is the angular radius of the central maxima which is mathematically represented as
is the angular radius of the central maxima which is mathematically represented as
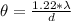
=>
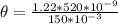
=>

Hence

=>

Generally linear diameter is mathematically represented as
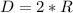
Where
 is the linear radius which is mathematically represented as
is the linear radius which is mathematically represented as
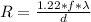
=>
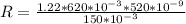
=>
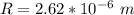
Thus