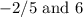Answer:
Explanation:
So we have the equation:
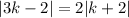
First, distribute the 2 into the absolute value:
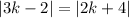
Definition of absolute value:
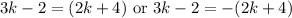
Left:
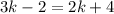
Subtract 2k from both sides:
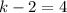
Add 2 to both sides:
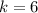
Right:
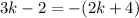
Distribute the negative:
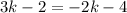
Add 2k to both sides:
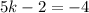
Add 2:
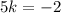
Divide by 5:
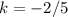
So, our solutions are: