Answer:
The complete sequence is: 1, 8, 29, 92, 281.
Explanation:
The series to be completed is:
1, _, _, _, _
The information provided is:
- The first term in the sequence is 1.
- Each other term is 5 more than three times the previous term.
Then the nth term can be determined using the expression:
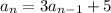
Compute the 2nd, 3rd, 4th and 5th term as follows:
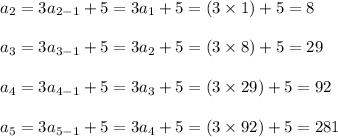
Thus, the complete sequence is:
1, 8, 29, 92, 281.