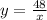Question

When x=3 ,y=16 and when x=6 y=8. Which inverse variation equation can be used to model this function?

Answer 1

The inverse variation equation can be used to model this function is:

`y=(48)/(x)`

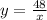
Explanation:

An inverse relationship between two variables implies that if the value of one variable increases the value of the other variable will decreases and vice-versa.

The inverse function describing the relationship between x and y is as follows:

`y=(a)/(x)`

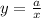
Here, a is a constant.

It is provided that when the value of x is 3 the value of y is 16.

Compute the value of a as follows:

`y=(a)/(x)`

`16=(a)/(3)\\\\`

`a=48`

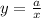
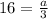
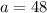
It is also provided that when the value of x is 6 the value of y is 8.

Compute the value of a as follows:

`y=(a)/(x)`

`8=(a)/(6)\\\\`

`a=48`

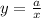
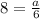
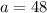
The value of a is 48.

Then the inverse variation equation can be used to model this function is:

`y=(48)/(x)`

Answer 2

`y=(48)/(x)`

Explanation:

When x = 3, y = 16

When x = 6, y = 8

We need to model the inverse variation.

Inverse Variation : When one value increase another value decrease. But product of both always constant.

`xy=k`

when x=3, y=16

k=48

When x=6, y=8

k=48

Model of the inverse variation:

`y=(48)/(x)`

Hence, The model of inverse variation is

`y=(48)/(x)`