Answer:
The length of the arc is
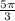 centimeters.
centimeters.
Explanation:
The length of an arc (
 ) with a given central angle is determined by the following expression:
) with a given central angle is determined by the following expression:

Where:
 - Radius, measured in centimeters.
- Radius, measured in centimeters.
 - Central angle, measured in sexagesimal degrees.
- Central angle, measured in sexagesimal degrees.
Given that
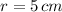 and
and
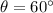 , then:
, then:

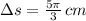
The length of the arc is
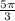 centimeters.
centimeters.