Answer:
B
Explanation:
So we have:
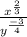
First, we recall that we can switch an exponent from the denominator to the numerator if we multiply the exponent by -1 and vice versa. Therefore:
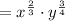
Now, use the following property:
![a^(x/n)=\sqrt[n]{a^x}](https://img.qammunity.org/2021/formulas/mathematics/college/pmmyrirpc4f23sadqys5fo838bux5d2icj.png)
Therefore:
![x^{(2)/(3)}=\sqrt[3]{x^2}](https://img.qammunity.org/2021/formulas/mathematics/college/iiho3pg6dgyz9iictnaupje5fp9264do1w.png)
And:
![y^{(3)/(4)}=\sqrt[4]{y^3}](https://img.qammunity.org/2021/formulas/mathematics/college/g644xsdmstr71g3gogyob6ru9nrt8sn991.png)
And so together:
![=x^{(2)/(3)}}\cdot {y^{(3)/(4)}\\=\sqrt[3]{x^2}\cdot\sqrt[4]{y^3}](https://img.qammunity.org/2021/formulas/mathematics/college/v3p3fsrky6zectuvlnynshpia0e1xf7c4b.png)
Our answer is B :)