2 Answers

Simone Porcu · Answer 1 · 2021-12-23T05:26:57+0000

Answer:

B

Explanation:

So we have:

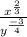
$\frac{x^{(2)/(3)}}{y^{(-3)/(4)}}$

First, we recall that we can switch an exponent from the denominator to the numerator if we multiply the exponent by -1 and vice versa. Therefore:

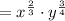
$=x^{(2)/(3)}}\cdot {y^{(3)/(4)}$

Now, use the following property:

$a^(x/n)=\sqrt[n]{a^x}$

Therefore:

$x^{(2)/(3)}=\sqrt[3]{x^2}$

And:

$y^{(3)/(4)}=\sqrt[4]{y^3}$

And so together:

$=x^{(2)/(3)}}\cdot {y^{(3)/(4)}\\=\sqrt[3]{x^2}\cdot\sqrt[4]{y^3}$

Our answer is B :)

Please log in or register to add a comment.