Question

Find the deriative dy/dx for y=x^2-2x/x^3+3

Answer 1

`(dy)/(dx)=(((2x-2)(x^3+3)-(x^2-2x)(3x^2))/((x^3+3)^2))`

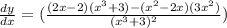
Explanation:

So we want to find the derivative of the rational equation:

`y=(x^2-2x)/(x^3+3)`

First, recall the quotient rule:

`((f)/(g))'=(f'g-fg')/(g^2)`

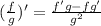
Let f be x^2-2x and let g be x^3+3.

Calculate the derivatives of each:

`f=x^2-2x\\f'=2x-2`

`g=x^3+3\\g=3x^2`

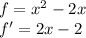
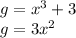
So:

`(dy)/(dx)=((x^2-2x)/(x^3+3))'`

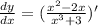
Use the above format:

`(dy)/(dx)=(f'g-fg')/(g^2)\\(dy)/(dx)=(((2x-2)(x^3+3)-(x^2-2x)(3x^2))/((x^3+3)^2))`

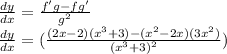
And that's our answer :)

(If you want to, you can also expand. However, no terms will be canceled.)