Answer:
(i) The period is 0.25 seconds, (ii) The angular velocity is approximately 25.133 radians per second, (iii) The linear velocity of the particle is approximately 50.266 meters per second, (iv) The acceleration experimented by the particle is approximately 1263.336 meters per square second.
Step-by-step explanation:
(i) Let suppose that particle experiments an uniform circular motion. The period (
 ) of the particle, measured in seconds, is the time needed to complete a revolution, which is determined by this:
) of the particle, measured in seconds, is the time needed to complete a revolution, which is determined by this:
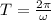
Where
 is the angular speed, measured in radians per second.
is the angular speed, measured in radians per second.
Let is convert angular speed from revolutions per minute into radians per second:
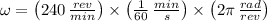

The period of the particle is:


The period is 0.25 seconds.
(ii) The angular velocity is approximately 25.133 radians per second.
(iii) The linear velocity of the particle (
 ), measured in meters per second, is found by this expression:
), measured in meters per second, is found by this expression:
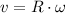
Where:
 - Radius, measured in meters.
- Radius, measured in meters.
 - Angular velocity, measured in radians per second.
- Angular velocity, measured in radians per second.
If
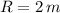 and
and
 , the linear velocity of the particle is:
, the linear velocity of the particle is:
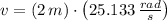
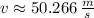
The linear velocity of the particle is approximately 50.266 meters per second.
(iv) As particle rotates at constant speed, resultant acceleration (
 ) is entirely radial and modelled by this expression:
) is entirely radial and modelled by this expression:
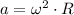
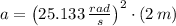
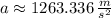
The acceleration experimented by the particle is approximately 1263.336 meters per square second.