Question

I WILL GIVE BRAINILEST!!! Elvira is interested in collecting data about how many students use each of the tables during each lunch period. She has recorded some data on Post-It Notes to analyze later. Here are the notes she has recorded: ● Some students are sitting at the front table. (I got distracted by an incident in the back of the lunchroom,and forgot to record how many students.) ● Each of the students at the front table has been joined by a friend, doubling the number of students at the table. ● Four more students have just taken seats with the students at the front table. ● The students at the front table separated into three equal-sized groups. One group remained and all the other students left. ● As the lunch period ends, there are still 12 students seated at the front table. a) Create an equation and solve it to answer the above question. b) If the bullet points were in a different order, would the equation and answer still be the same? Use an example to help explain your answer.

Answer 1

yes

Explanation:

2 plus 2 is 4

Answer 2

The initial number of students at the front table is 16. The equation and answer remain the same regardless of the order of the bullet points, as they express consistent relationships.

a) Creating and solving the equation:

Let x represent the initial number of students at the front table.

1. Some students are sitting at the front table: x students.

2. Each student at the front table has a friend: 2x students.

3. Four more students join: 2x + 4 students.

4. The front table separates into three equal-sized groups:
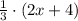`\( (1)/(3) \cdot (2x + 4) \)` students.

5. One group remains, and the rest leave:
`\( (1)/(3) \cdot (2x + 4) = 12 \)` students.

Now, solve for x:

`\[ (1)/(3) \cdot (2x + 4) = 12 \]`

2x + 4 = 36

2x = 32

x = 16

Therefore, the initial number of students at the front table was x = 16.

b) Impact of different order of bullet points:

The order of the bullet points does not affect the equation or the answer. The equation is based on the relationships between the different stages, regardless of their order.

For example, if the bullet points were rearranged:

1. Some students are sitting at the front table.

2. Four more students have just taken seats with the students at the front table.

3. Each student at the front table has a friend, doubling the number of students at the table.

4. The students at the front table separated into three equal-sized groups. One group remained, and all the other students left.

5. As the lunch period ends, there are still 12 students seated at the front table.

The resulting equation and solution would still be the same because we are expressing the same relationships between the number of students at different stages, regardless of the order in which they are presented.