Question

How do you do this Please Explain how you did

Answer 1

Domain : (- ∞, - 5), and (3 / 2, ∞),

Range : (∞, 0.4437]

Explanation:

Assuming that we want our answer in interval notation, let's start by determining the domain. Remember that the domain can be found where the function is undefined.

Given : f(x) = (2x - 7) / (2x² + 7x - 15)

Alternative Form : (2x - 7) / (x + 5)(2x - 3)

To receive this 'alternative form' we can simply factor the expression 2x² + 7x - 15. See the procedure below,

`\mathrm{Given : 2x^2+7x-15} ,`

`\mathrm{Break\:the\:expression\:into\:groups : \left(2x^2-3x\right)+\left(10x-15\right)} ,`

`\mathrm{Factor\:out\:}x\mathrm{\:from\:}2x^2-3x\mathrm{:\quad }x\left(2x-3\right),\\\mathrm{Factor\:out\:}5\mathrm{\:from\:}10x-15\mathrm{:\quad }5\left(2x-3\right),`

`x\left(2x-3\right)+5\left(2x-3\right) = \left(2x-3\right)\left(x+5\right) - \mathrm{Factored\:expression}`

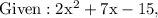
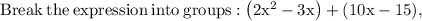
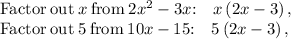
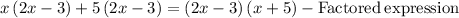
Now let's find the domain using the expression '(x + 5)(2x - 3) = 0.' If the denominator equals 0, the function is considered undefined.

`\mathrm{Given : \left(x+5\right)\left(2x-3\right)=0} ,\\x+5=0:\quad x=-5, 2x-3=0:\quad x=(3)/(2)\\\mathrm{The\:solutions\:are: x=-5,\:x=(3)/(2)}`

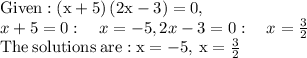
Knowing these solutions the domain has the intervals (- ∞, - 5), and (3 / 2, ∞). The range is the set of values that correspond to the domain, so in this case the range would be (∞, 42 + 8√17 / 169]. 42 + 8√17 / 169 = (About) 0.4437, so it lies on the interval (∞, 0.4437].

The images below represent the plotted function in two areas. There are 3 curves in this graph.