Question

22. Find three consecutive odd numbers such that the sum of five times the smaller number and twice

the larger number is 33 more than six times the median number.

Answer 1

The numbers are 37, 39 and 41.

Explanation:

Let the smallest number be
`x\\`.

Then the other numbers will be
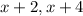`x+2, x+4` (as they are consecutive odd numbers, their difference will be 2).

As per the given statement:

LHS(Left Hand Side) : Sum of five times the smaller number and twice the larger number.

i.e. five times the smaller number =
`5* x`

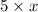
twice the larger number =
`2 * (x+4)`

Their sum:

The Left Hand Side becomes:

`5x+2(x+4)`

RHS(Right Hand Side):

33 more than six times the median number:

i.e.
`6*(x+2) +33`

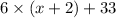
Equating LHS and RHS:

`5x+2(x+4) = 6x+12 +33\\\Rightarrow 7x+8=6x+47\\\Rightarrow \bold{x =37}`

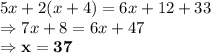
Therefore, the numbers are 37, 39 and 41.