Answer: (a) BE = 1.112 MeV
(b) BE = 7.074 MeV
(c) BE = 7.767 MeV
(d) BE = 8.112 MeV
Explanation: Binding energy per nucleon is the average energy necessary to remove a proton or a neutron from the nucleus of an atom. It is mathematically defined as:
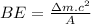
Where
Δm is a difference in mass known as mass defect
A is atomic mass of an atom.
Mass Defect is determined by:

where:
Z is atomic number
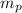 is mass of proton
is mass of proton
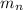 is mass of neutron
is mass of neutron
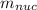 is mass of the nucleus
is mass of the nucleus
Mass of proton is 1.007825u.
Mass of neutron is 1.008665u.
The unit u is equal to 931.5MeV/c².
(a) 2H(deuterion): Given: Z = 1; A = 2;
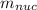 = 2.014102u
= 2.014102u
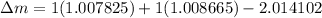
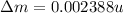
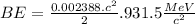
BE = 1.112MeV
(b) 4He (Helium): Given: Z = 2; A = 4;
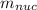 = 4.002603
= 4.002603


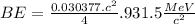
BE = 7.074MeV
(c) 18O (Oxygen): Given: Z = 8; A = 18;
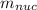 = 17.999160
= 17.999160

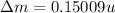
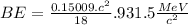
BE = 7.767MeV
(d) 23Na (Sodium): Given: Z = 11; A = 23;
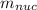 = 22.989767
= 22.989767
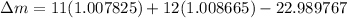
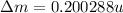
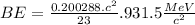
BE = 8.112MeV