Question

Let A and B be n-by-n matrices in R^n, and let c be a real number. Which of the following statements about trace is not necessarily true? a. tr(A+B) = tr(A) + tr(B) b. tr(AB) = tr(BA) c. tr(AB) = tr(A)tr(B) d. tr(CA) = ctr(A)

Answer 1

c. tr(AB) = tr(A)tr(B)

Answer 2

c. tr(AB) = tr(A)tr(B)

Explanation:

The trace of a matrix is only valid for a square matrix, that is a n by n matrix. The trace of a matrix is the sum of all its diagonal elements. The following properties of trace holds for a matrix A and B with size n by n and a real number c.

i) The trace sum of two matrix is equal to the sum of their individual traces. That is:

tr(A + B) = tr(A) + tr(B)

ii) The trace of the product of a scalar and a matrix is the same as the product of the scalar and the trace of the product, that is:

tr(cA) = ctr(A)

iii) The trace of a transpose of a matrix is equal to the trace of the matrix, that is:

`tr(A^T)=tr(A)`

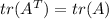
iv) The trace of a product of matrix is given as:

tr(AB) = tr(BA)