Question

7)

The first floor of the Willis Tower is 21 feet high. Each additional floor is 12 feet high.
a
Write an equation for the nth floor of the tower.
b.
Find the height of the 65th floor.

Answer 1

Explanation:

If the first floor of the Willis Tower is 21 feet high. and each additional floor is 12 feet high, then the floor heights as we move from one floor to another we keep increasing by 12feets and forms an arithmetic progression as shown;

21, (21+12), (21+12+12), ...

21, 33, 45...

a) To write an equation for the nth floor of the tower, we will have to find the nth term of the sequence using the formula for finding the nth term of an arithmetic sequence.

The nth term of an arithmetic sequence is expressed as
`T_n = a + (n-1)d`

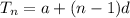
a is the first term = 21

d is the common difference = 33-21 = 45-33 = 12

n is the number of terms

Substituting the given parameters into the formula;

`T_n = 21+(n-1)*12\\T_n = 21+12n-12\\T_n = 21-12+12n\\T_n = 9+12n`

Hence the equation for the nth floor of the tower is expressed as
`T_n = 9+12n`

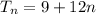
b) To get the height of the 65th floor, we will substitute n = 65 into the formula arrived at in (a)

`T_n = 9+12n\\T_(65) = 9 + 12(65)\\T_(65) = 9+780\\T_(65) = 789 ft`

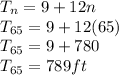
Hence the height of the 65th floor is 789feets.