Answer:
The interest rate on the account is 2.1%
Explanation:
Compound interest is one that is added to the initial capital and on which new interests are generated. Money, in this case, has a multiplier effect because interest produces new interest. In other words, the initial capital increases in each period because the interests add up.
To calculate the final capital, the initial capital is multiplied by one plus the interest, raised to the number of periods:
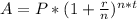
where
- A = Accumulated amount (principal + interest)
- P = Principal amount
- r = the interest rate
- n = the number of times the interest is compounded per year
- t = Time Involved in years
In this case:
- A = $3,439.96
- P = $3,104.31
- r = ?
- n = 4
- t = 5
Replacing, you get:
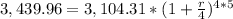
Now, solving:
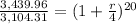
![\sqrt[20]{1.1081} =(1+(r)/(4))](https://img.qammunity.org/2021/formulas/mathematics/high-school/5p7tqjswhfaou6pjc5ac05ds8anie3md7i.png)
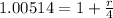
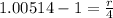

r=0.0051*4
r= 0.02056
In percentage it is expressed as: r= 2.056 %≅ 2.1 %
The interest rate on the account is 2.1%