Question

1. How does the de Broglie wavelength of an electron change if its momentum increases?

a. The de Broglie wavelength of the electron increases.
b. The de Broglie wavelength of the electron decreases.
c. The de Broglie wavelength of the electron is unchanged.
2. How does the de Broglie wavelength of an electron change if its kinetic energy decreases?
a. The de Broglie wavelength of the electron increases.
b. The de Broglie wavelength of the electron decreases.
c. The de Broglie wavelength of the electron is unchanged.

Answer 1

1. The de Broglie wavelength of the electron decreases if its momentum increases.

b. The de Broglie wavelength of the electron decreases is the correct answer

2. The de Broglie wavelength of the electron increases as the kinetic energy decreases.

a. The de Broglie wavelength of the electron increases is the correct option

Step-by-step explanation:

1. The relationship between de Broglie wavelength, λ and momentum ρ is given by

λ = h/ρ

Where λ is the de Broglie wavelength

h is Planck's constant and

ρ is the momentum

From the formula, the de Broglie wavelength, λ varies inversely with the momentum, ρ. Hence, as the de Broglie wavelength increases the momentum decreases; similarly, as the de Broglie wavelength decreases, the momentum increases.

For question 1, The de Broglie wavelength of the electron decreases if its momentum increases.

b. The de Broglie wavelength of the electron decreases is the correct answer

2. From

λ = h/ρ

ρ = mv

∴ λ =
`(h)/(mv)`

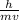
Where m is mass

and v i velocity

Recall that Kinetic energy K.E is given by

K.E =
`(1)/(2)mv^(2)`

`E_(K) = (1)/(2)mv^(2)`

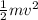
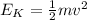
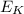`E_(K)` is the kinetic energy

∴
`v = \sqrt{(2E_(K) )/(m) }`

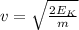
Now we will evaluate
`mv`

`mv = m \sqrt{(2E_(K) )/(m) }\\mv = \sqrt{m^(2) }.\sqrt{(2E_(K) )/(m) }\\ mv = \sqrt{(2m^(2)E_(K) )/(m) } \\mv = \sqrt{{2mE_(K) }`

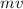
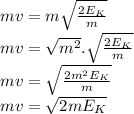
∴ λ =
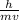`(h)/(mv)` becomes

λ =
`\frac{h}{\sqrt{2mE_(K) } }`

This equation shows the relationship between the de Broglie wavelength and kinetic energy,
`E_(K)`

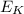
From the equation, de Broglie wavelength varies inversely with kinetic energy. That is, as the de Broglie wavelength increases the kinetic energy decreases; similarly, as the de Broglie wavelength decreases, the kinetic increases.

For question 2, The de Broglie wavelength of the electron increases as the kinetic energy decreases.

a. The de Broglie wavelength of the electron increases is the correct option