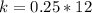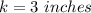Question

A 25 foot long rectangular sheet of metal, 12 inches wide, is to be made into a rain gutter by turning up two sides so that they are perpendicular to the sheet. How many inches should be turned up to give the gutter its greatest capacity?

Answer 1

The value is
`k = 3 \ inches`

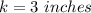
Explanation:

From the question we are told that

The length is
`l = 25 \ ft`

The width is
`w = 12 \ inches = (12)/(12) = 1\ ft`

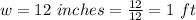
Generally let assume that (k ft) was turned up on each side hence the remaining width is

`(1 - 2 k ) \ ft`

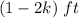
Now the capacity is also the volume it can hold which is mathematically represented as

`C = 25 (1- 2k) k`

`C = 25 (k- 2k^2)`

`C = 25k - 50k^2`

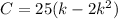
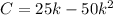
At maximum or minimum

`(dC)/(dk) = 0`

=>
`(dC)/(dk) = 25 - 100k = 0`

=>
`k = 0.25\ ft`

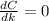
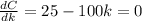
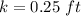
Now to see if the value obtained is positive or negative we differentiate a second time

So

`(d^2C)/(dk^2) = - 100k`

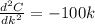
at k = 0,25 ft

`(d^2C)/(dk^2) = - 100(0.25)`

`(d^2C)/(dk^2) = -25`

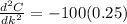
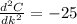
since a negative value is obtained then k is the maximum value

converting to inches

`k = 0.25 * 12`

`k = 3 \ inches`