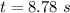Answer:
The time is
Step-by-step explanation:
From the question we are told that
The initial height of the eye is
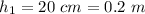
The height of the eye when you jumped up is
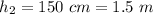
An illustration of this question is shown on the first uploaded image
Generally the radius of the earth is
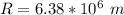
Now from the diagram first sun means first time you saw the sun and the second sun means second time you saw the sun then
H is the height increase when you quickly stood up which is mathematically evaluated as
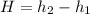
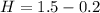
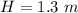
Also
 i the angular displacement between the first and second position and from geometry it is also the angle at one of the sides of the right angle triangle
i the angular displacement between the first and second position and from geometry it is also the angle at one of the sides of the right angle triangle
Applying Pythagoras theorem

=>
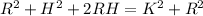
Now given that H is very small compared to R the we ignore

So
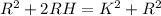
=>
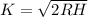
=>
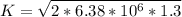
=>
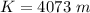
Now the
 is mathematically evaluated using SOHCAHTOA as follows
is mathematically evaluated using SOHCAHTOA as follows
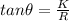
![\theta = tan^(-1)[ (K)/(R)]](https://img.qammunity.org/2021/formulas/physics/high-school/27oyx3mr8wsm9opce13le88189k2igl9yi.png)
=>
![\theta = tan^(-1)[ ( 4073)/(6.38*10^(6))]](https://img.qammunity.org/2021/formulas/physics/high-school/qs5nfmxfgvlom9jz2138fx9gwag9eqe81u.png)
=>
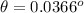
Generally
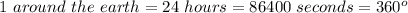
So
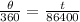
=>
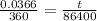
=>