Answer:
-26
Explanation:
Given the sequence:
16, 9, 2, –5, ...,
To find:
7th measurement, if the above sequence continues:
Solution:
Let us examine the given sequence first:
First term is 16
Second term = 9
Third term = 2
Fourth term = -5
Difference between 2nd and 1st term = 9 - 16 = -7
Difference between 3rd and 2nd term = 2 - 9 = -7
Difference between 4th and 3rd term = -5 - 2 = -7
We can see that there is a common difference of -7 between each term.
That means, the sequence is in Arithmetic Progression.
whose first term,
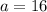
Common difference,
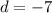
To find:
7th term i.e.
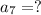
Solution:
Formula for
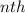 term of an Arithmetic Progression is given as:
term of an Arithmetic Progression is given as:

Let us put
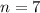
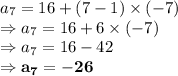
7th measurement will be -26.